Ali Fisunoğlu
Carlos III – Juan March Institute of Social Science
This article provides an introduction to system dynamics modeling with a particular focus on the use of system dynamics models in political science and international relations. A system dynamics approach offers an alternative to traditional qualitative and quantitative methods by providing a dynamic and endogenous point of view, which allows for understanding the dynamic interactions between variables and making short- and long-term projections for alternative policy choices. This approach is particularly useful to tackle the complex problems of contemporary politics, in which the solutions require combining the insights from different disciplines. Applications of a system dynamics approach in the social sciences cover a broad spectrum, from war initiation and termination to social inequality, from demographics to human development and democratization. This article starts by presenting the brief history of system dynamics models and their use in social sciences, and comparing a system dynamics approach to traditional qualitative and quantitative research methods by discussing the advantages and disadvantages of each one. This discussion is followed by the explanation of the essential components of system dynamics models. Finally, the article provides several applications from international relations via developing models of arms races and spread of intrastate conflicts.
1.Introduction
With the proliferation of inexpensive computing power, the role of modeling and simulations in social science has been growing at a dramatic pace. The increasingly complex dynamic problems of contemporary world politics require increasingly complex and dynamic (re)actions and solutions. System dynamics modeling provides a useful tool to tackle the intricate problems that the world faces today.
The system dynamics approach is different from traditional quantitative methods. Traditional statistical methods often define the dependent variable as a function of several independent variables and test the relationship between these variables using data. These models can demonstrate statistical correlations and enable us to make short-term forecasts based on non-causal correlational relationships. The system dynamics approach, on the other hand, is based merely on causal relations. Through understanding the causal mechanisms, the system dynamics approach provides us a tool to understand and manipulate dynamic problems. For this reason, traditional stochastic or econometric models of political phenomena are being supplemented more and more by dynamic simulation methods drawn from multidisciplinary perspectives.
Let’s start the examination of system dynamics models by defining what a system is and discussing the benefits of using a system dynamics approach rather than more traditional approaches. According to the Oxford English Dictionary, a system is “a set of things working together as parts of a mechanism or an interconnecting network; a complex whole.”[1] System dynamics studies the dynamics of the systems and interconnection of their pieces.
Many questions in political science and international relations can be explained using a system dynamics approach. Elements of politics and international relations affect each other. For an illustration, consider the politics of the international monetary system. An interest rate hike by one country, especially if that country is one of the major economies such as the United States, causes a chain reaction in the exchange rates and interest rates of all other countries. This, in return, affects the balance of payments of countries, production, domestic and international winning coalitions, and so on. Thus, we know that all the different aspects of international politics influence each other. There are some aspects within the system that are endogenous, that is, the internal structure of the system directly causes them. Thus, we may be able to change or manipulate these endogenous elements to influence the outcome. There are also some aspects that are exogenous, or outside the system. The system dynamics approach models these endogenous and exogenous relations and analyzes the interrelationship and feedback mechanisms between different factors. System dynamics modeling takes the principles of physics and engineering and applies them to various other disciplines including social and administrative sciences as well as business management, demography, education and healthcare, energy and environmental policy, medical sciences, public policy, urban planning, and many other disciplines.
Why do we need system dynamics and systems thinking? To answer this question, we can focus on the classic argument that we live in a world that is rapidly changing. Things are accelerating, and relationships are becoming increasingly complex. Although this is true and systems thinking helps us survive and thrive in this complex world, there are other contributions of the system dynamics approach to the academic and policy worlds. In spite of the many new analytical tools and advanced methods that we have, we see that many policies that we implement are either failing or are creating unexpected side effects or adverse consequences. System dynamics models are particularly useful in these settings. Without a systems perspective, there is a higher likelihood of breaking or damaging one thing while trying to fix or improve another. Using the system dynamics approach, we can see the relationships clearly and become better problem solvers in a complex environment. Understanding the system that underlies the patterns that underlie the events we see from above allows us to solve problems and manipulate policies at each level.[2]
2. The System Dynamics Approach
System dynamics is a computer-aided approach to policy analysis and design. It applies to dynamic problems arising in complex social, managerial, economic, or ecological systems -- literally to any dynamic system characterized by interdependence, mutual interaction, information feedback, and circular causality. It can be related to and combined with formal models, like game theory, and extended to agent-based and computational models such as knowledge-based systems and machine learning.
The history of the system dynamics approach in social and political research is parallel to the history of research involving nonlinearity. It is hard to point to an exact date of origin, but significant contributions started to be made in the 1950s and 1960s by mathematical sociologists like Herbert Simon[3] and James Coleman,[4] and computer scientists like Jay W. Forrester.[5] The use of dynamic models in the social sciences accelerated with advances in mathematics, the broader application of these models in related fields such as population biology,[6] and the increased availability of data and computers.[7]
Continually increasing computing power and the ready availability of computers has allowed the social sciences, like the physical sciences, to employ more complex and technical research designs. We see an increase in the number of quantitative studies in social sciences especially during and after the 1970s.[8] However, the majority of the earlier (and current) social and political science theories and models employ a linear, and sometimes even a binary, approach.
The “hegemony of linear models” in political science is the result of a path-dependent trend caused by the historical dominance of linear models and the way social science data are collected. Consequently, the sociological imprint of linear models in the social sciences is still significant.[9] Linear models have been dominant in political science research, especially in quantitative studies, because the researchers historically have been constrained by their mathematical skills and the prevalent technology of their time. In the 1970s, when empirical social science became widespread, linear algebra was state of the art. Nevertheless, linear models are algebraically easier and more manageable than nonlinear, complex models. Moreover, between the 1960s and 80s, computers, which greatly assist in solving these complex models, had extremely limited computational abilities and were difficult to be accessed by most researchers. Therefore, social scientists had to be restricted to using the basic linear model, which provided a sufficient explanatory power. Also, calculating the main parameters (i.e., slopes) of the linear model was easy, and even slow computers could estimate these parameters quickly using relatively simple computer codes.
The second reason linear models are still dominant in political science is related to the way social and political science data are collected and structured. One issue with the data is that only a small number of the existing datasets have a sufficiently long range to allow for observing nonlinear trends. Except for some measures, many datasets that are frequently used do not extend back before the 1990s or 1980s.[10] Considering the slow-changing nature of many political and social phenomena, one would need a much longer temporal dimension to assess the nonlinear dynamics. The second issue with the data is that most data are collected in a focused and isolated way. Thus, datasets often do not provide information about the environment and the social context within which the data is formed. For instance, most surveys only inquire about some basic demographic information but fail to provide information about the local, national, or the global context. However, to be able to evaluate the dynamics accurately, we would need to have information regarding how our level of analysis interacts with the context with which it is involved.
Despite the fact that we often use linear models, hardly ever anything in the universe or political science is actually completely linear. Thus, statistics, regression analysis, and econometrics are inherently biased as we regularly measure nonlinear continuous time processes at two points, difference the variables, and evaluate a model/coefficient fit based upon it.
Another alternative to using linear models (and system dynamics modeling) is to use traditional qualitative techniques. Qualitative research provides a detailed description of events and cases of interest and presents a vibrant and holistic picture that focuses on naturally occurring events in their natural settings and allows for the study of processes, of how and why things happen the way they do. Since the subject of interest is studied in detail, influences of context are not stripped away. Therefore, tests of causality and chronological flow can be carried out. These characteristics alleviate the problems of linear models and capture the nonlinear nature of events. Moreover, the holistic approach of qualitative research can generate unexpected, unforeseen findings and new integrations and interpretations.
However, there are several downsides of qualitative research. Conducting qualitative studies is generally time-consuming and labor intensive. The detailed and holistic approach requires digesting an overload of data by the researcher, which makes the quality of the research dependent on a researcher’s attributes and skills and might inject subjectivity in the analysis. Moreover, since qualitative studies generally focus on a small sample of cases, they are often unable to aggregate data and make systematic comparisons, which cause these studies to lack generalizability. In addition, since precise definitions of the concepts analyzed need not be provided, issues of reliability and validity emerge, which might bring doubts on the credibility and quality of findings.
System dynamics modeling incorporates some of the advantages of qualitative and linear quantitative models and ameliorates most of their disadvantages. In systems dynamic modeling, the concepts are precisely defined so that the communication among scholars is unambiguous. The assumptions are clear so that the limitations of the models are apparent. The logical structure of the models provides an extensive guide for making formal deductions. System dynamics models alleviate the linearity constraint by taking into account the linear or nonlinear continuous path for each variable. Moreover, through system dynamics, we can talk about and analyze the evolution of various variables together in a system that we are interested in as well as the evolution of the system itself. The ability to evaluate the dynamics of a set of variables is especially convenient when anticipating the changes is useful in a puzzlingly complex system with very scarce data. We can easily create a deterministic model to represent a system and introduce uncertainty by using stochastic differential equations or running Monte Carlo Simulations. In this regard, although a system dynamics model is built to represent the reality, it is not constrained by reality. This characteristic makes system dynamics models beneficial for theory development and enables them to study rare-occurring events, such as the spread of civil war into another civil war. It also grants some generalizability to the models and allows for simulating different scenarios, providing clear implications for policy actions.
Undoubtedly, system dynamics models are still models, and thus are simplifications of the reality. “All models are wrong.” Only the reality is the reality, and any model that we develop will be a limited, imperfect representation. A model’s accuracy and its predictive power highly depend on its assumptions. If we start modeling with inappropriate assumptions, the results of our model will be invalid. Given its highly deductive structure, system dynamics models provide high internal and low external validity. Also, given the nature of complex models, it is challenging to test the process validity. Finally, the advantage of the versatility of system dynamics models can turn into a disadvantage if we start building “garbage in, garbage out” models with little theoretical basis and scientific value. A system dynamics model can become very complex when lots of factors and variables are modeled. In these cases, using different simulation techniques, such as Agent-Based Models (ABMs) can provide better results, although ABMs also suffer from the weaknesses above.
Any issue or question that includes emergence and a long-term equilibrium can be analyzed using system dynamics modeling. Most social processes fit this description. In comparison with linear methods, system dynamics modeling has a superior ability to represent the dynamic aspects of change. Thus, one can benefit from system dynamics modeling when studying almost any social science question. With the increasing availability of more extended time-series data that incorporates more extensive information, coupled with the advancing technical and computational capabilities of the researchers, the utilization of dynamic models will likely be more frequent in social sciences.
The approach begins with defining problems dynamically, proceeds through mapping and modeling stages, to steps for building confidence in the model, and its policy implications. After identifying the problems, one should advance to the modeling and simulation stages. Mathematically, the basic structure of a formal system dynamics model is a system of coupled, nonlinear, first (or higher) order differential (or integral) equations. Simulation of such systems is easily accomplished by partitioning simulated time into discrete intervals of length dt and stepping the system through time one dt at a time.
Here, let’s consider what a system is and why we are using a system of equations rather than using a single equation. A system is a set of interrelated, interacting, or interdependent components.[11] The system is essentially a conceptual construction. Yet, there are some common properties of each system. Systems are hierarchical structures. They can include sub-systems or different levels (integrations). The components (variables) of the system demonstrate different and distinct behavior over time as they interact with each other.
Since we are interested in how interrelated actors or variables within the system behave and the evolution of their behavior together in a system, we often define systems as a set of equations. Using a set of equations signifies that we are not limited by the single equation or linear logic of traditional statistics. This also means that we do not have to misrepresent the deductions of the social theory due to algebraic requirements of statistical models.[12] We are interested in explaining and predicting the complex, interactive behavior of different elements of our theory, so a system captures these types of phenomena. Moreover, solving a single equation requires the same tools as solving a set of equations. All we do is write nonlinear system in terms of derivative and then solve numerically, with some approximation technique – Euler, 4th order Runge-Kutta, Bursch-Stoller, etc.
Another property of systems is that they can be symmetric or asymmetric. A symmetric system consists of equations with the same algebraic structure. An asymmetric system includes equations with different algebraic structures. Whether a system is symmetric or asymmetric has no implications for the generalizability or theoretical value of the models. Despite the majority of the social science questions involve asymmetric systems, symmetric systems can generate unexpected and novel results as well.
Overall, several principal notions characterize the system dynamics approach.[13] First, dynamic thinking is at the center of system dynamics models. System dynamics approach examines concepts over time, which enables the analysis of their evolution. The system dynamics approach emphasizes a continuous view. The continuous view strives to look beyond events to see the dynamic patterns underlying them. Moreover, the continuous view focuses not on discrete decisions but the policy structure underlying decisions. Events and decisions are seen as surface phenomena that ride on an underlying tide of system structure and behavior. Thus, the behavior of actors and factors are a consequence of the structure of the system. The most common way of demonstrating the dynamic and continuous aspects of the variables is to use time series graphs.[14]
Second, stocks (levels) and the flows (rates) that affect the stocks are essential components of the system structure. That is, the models focus on the initial level and growth or decrease over time. Stocks (accumulations, state variables) are the memory of a dynamic system, and flows (positive or negative accumulations and their rates of change) are the sources of its disequilibrium and dynamic behavior.
Third, system dynamics thinking accentuates causation rather than correlation. In the system dynamics thinking, we are interested in the effect of one variable on the other variable. This effect, or the causation, is demonstrated using causal diagrams. In a causal diagram, arrows going from one variable to the other indicate the causal influence of one variable on the other variable. The positive and negative signs that are placed next to the arrows indicate a positive or a negative relationship (not addition and subtraction).
Fourth, conceptually, feedback and feedback loops are at the heart of the system dynamics approach. Feedback loops form (or exist) when decisions change the state of the system, which consequently changes the structure and information that affect future decisions.[15] Thus, it entails a back and forth exchange between the components (or the actors) of the system, causing the conditions and information that influence future actions to change. Consequently, the feedback loop implies circular causality.[16] Diagrams of loops of information feedback and circular causality are tools for conceptualizing the structure of a complex system and for communicating model-based insights. The loop concept underlying feedback and circular causality by itself is not enough, however. The explanatory power and insightfulness of feedback understanding also rests on the notions of active structure and loop dominance, which enable the user to derive nonlinear results. There are two types of feedback loops. Reinforcing loops cause infinite growth whereas balancing loops try to move the variable into the desired state.
Lastly, a system dynamics approach involves endogenous thinking and reckons system as the cause. It provides an endogenous point of view. The concept of endogenous change is fundamental to the system dynamics approach. It dictates aspects of model formulation: exogenous disturbances are seen at most as triggers of system behavior; the causes are contained within the structure of the system itself. So, the endogenous aspect of the system emerges from the notion of feedback.[17] According to the endogenous point of view, the root causes of an issue are not considered as exogenous forces appearing from outside. Instead, these causes are connected to the system using feedback loops, which endogenizes the sources of system behavior.
A system and the variables within the system can behave in several general ways. If a variable keeps increasing or growing over time, it means that it is demonstrating growth behavior. The growth behavior is observed when the positive, or reinforcing, feedback loop is consistently dominant. This growth can be linear or exponential, based on the magnitude of the impact of the feedback loop (yet, exponential growth is a more common pattern). Note that even when a variable is demonstrating growth behavior, there can still be multiple feedback loops affecting the variable, some positively and some negatively. If the variable shows growth behavior despite the presence of multiple feedback loops, which affect the variable on opposite directions, this means that the positive feedback loops are the dominant ones. The decay behavior has almost identical characteristics to the growth behavior. In the decay behavior, positive feedback loops are replaced with negative, balancing, feedback loops. The main difference is that there is often an implicit goal of zero, and the time it takes for the system to reach zero is called its half-life.
Another pattern of behavior is the goal seeking one. If a variable demonstrates goal seeking behavior, it means that it approaches a stable equilibrium over time. The goal seeking behavior is observed when the balancing feedback loop is dominant. In the real world and particularly in social systems, the system hardly ever reaches its goal of equilibrium, because random shocks happen frequently. For example, economic theory states that prices arrive at an equilibrium where supply and demand meet in a free market economy. However, in the real world, prices are not stable. They move around the equilibrium price. In a political-economic context, we can think about the goal-seeking behavior as inflation targeting.[18] Although the central bank sets a target inflation level, that target is rarely reached due to price shocks.
Oscillating behavior is another general behavior pattern observed in dynamic systems. It is typically caused by a balancing feedback with delays. This delay causes the rate of change of the system to be zero when the system moves from an increasing trend to a decreasing trend or a decreasing trend to an increasing trend. When this transition happens, there is a period of stock between two or more flows.[19] Based on the structure of the system, the oscillations are expected to diminish and reach equilibrium or increase in size and frequency. A social science example is the demographic consequences of the conflict. Major wars often cause youth bulges as a result of the disturbance they cause in the birth and death rates.[20] [21] It takes generations until the effect of conflict diminishes. These youth bulges have long-term economic and social effects, increasing the likelihood of long-term conflict.[22]
The last type of general behavior is the S-Curve or the limited growth. In a limited growth system, the magnitude of the effect of positive and negative feedback loops might be in near parity, or where the dominant loop changes over time. Yet, this might still result in a long-run equilibrium. Limited growth systems often start with the dominance of the positive feedback, which causes the system variable to increase exponentially. However, over time as the negative or balancing feedback starts dominating, the growth slows down, and the system reaches equilibrium. The majority of the spread or adoption models demonstrate an S-Curve pattern. As Schelling demonstrates, many social mechanisms, such as the spread of new ideas or adoption of new technologies demonstrate this pattern.[23] For instance, when a new idea emerges, people start talking about it if they are intrigued by it. The more people intrigued about it, the more people talk about it, which causes an exponential growth in the number of people exposed to this idea. However, since there is a limit to the number of people that can be exposed to this idea, the spread slows down over time and arrives at equilibrium. Through this process, the spread of the idea follows an S-Curve pattern. Another area where limited growth is observed is the demographic and economic transitions, which are key to the power based theories of war.[24] Historically, nations in preindustrial stages had low levels of productivity and population growth. As they are industrialized, they experience a significant spurt in their power as a result of increased productivity and population. However, as nations reach the stage of power maturity, both the productivity and the population growth decelerate and reach an equilibrium. The power transitions that result from these dynamic changes are one of the major causes of major power conflict.[25]
In addition to the aforementioned general patterns of behavior, a system can show different types of behavior at different times. We can observe different virtuous positive or negative circles, death spirals, growing or declining oscillatory patterns, things getting better before they start declining, or things getting worse before they get better. For instance, through dynamic modeling, we can see that third-party intervention in civil wars decreases the severity of the conflict in the short-term but causes the severity to increase in the long-term. The variety of patterns enables us to better understanding the system and underlying factors, gain more comprehensive insights, and make more accurate forecasts.
A system dynamics approach has been previously utilized in various physical as well as in social science settings. The majority of the system dynamic work in political science deals with the evolution of peace and conflict. Starting with Richardson’s seminal work on arms races and conflict,[26] numerous studies have been published that deal with war. Due to its emphasis on the importance of system dynamics, students of power transition theory developed several system dynamics models of conflict. For example, Abdollahian and Kang, as well as Kadera, demonstrate that the structural conditions, mainly power parity and the satisfaction with the status quo, are the primary determinants for war (or lack of war) in the international system. Also a member of the realist school of thought, Jervis[27] asserts that the anarchy in the international system is a result of its complex systemic structure, in which states compete for more power and security.
Several other studies also focused on the evolution of conflict or cooperation using a system dynamics approach. Kadera[28] develops a dynamic model of the spread (or “contagion”) of civil and interstate wars. She examines three principal components in the model. One component is the transmission mechanism, which covers factors such as geographic distance, openness and willingness to engage and other various ways international actors expose one another to conflict. The second component, barriers, deals with potential components that slow down the spread of conflict such as neutrality agreements, and the third component, resource constraints, is designed to capture the social welfare trade-off associated with military expenditures. Kadera finds that in all fifty simulation cases there was a positive equilibrium, suggesting that even if states endeavor to avoid the ongoing conflicts in a given region and do not get involved, they still cannot effectively stop the spread of war. Kadera’s dynamic model also reveals that systemic characteristics of contagion are expected to move regional engagement towards a positive equilibrium, forcing regional actors to participate. The results also suggest that aggregate amount of war in a system decreases as barriers are replaced with transmission mechanisms. Overall, lowering the number of interactions in the system reduces the spread of war.
In a more recent study, Kadera and Morey[29] develop the fighting versus investing model and demonstrate that weaker countries are better off when they fight a counterforce war and that targeting industrial production facilities rather than military forces shortens the war and decreases the likelihood of a stalemate. For several other important studies that employ dynamic models on interstate war, see Zinnes and Muncaster,[30] Abdollahian, Baranick, Nicholson, and Nickens,[31] and Morey.[32]
As a result of the US invasion of Iraq and global increase in terrorist activities,[33] the last 15 years have seen an increase in the number of studies focusing on civil war, insurgency, and terrorism. Let’s consider a dynamic model of terrorist recruitment, as developed by Faria and Arce.[34] According to the model, at time 0, a terrorist organization has a certain number of militants, which would be the stock variable. Terrorist organizations can recruit new members amongst the population. Recruitment is expected to be easier if there are more hard-core believers of the organization's ideology and if the overall public support to the organization is high. Recruitments can be curtailed using liberal values such as increasing democracy or reducing oppression, or increasing economic activities or well-being. Alternatively, governments can choose deterrence strategies through the use of security forces or punishments. The results of Faria and Arce’s model indicate that liberal measures are more successful at decreasing terrorist recruitment through their impact on public support whereas deterrence policies decrease the recruitment of fanatics. Elimination of terrorism in the long run is possible if the counter-terrorism measures are affordable and the number of hard-core supporters is not large.
For several other important studies that employ dynamic models on intrastate war, terrorism, and insurgency see Hoover and Kowalewski,[35] Chamberlain,[36] Blank, Enomoto, Gegax, McGuckin, and Simmons,[37] Banks and Sokolowski,[38] Kadera and Kim.[39]
Dynamic models cover a wide range of other areas in political science and international relations including, but not limited to, the evolution of democracy and values,[40] [41] electoral politics,[42] [43] and environmental politics.[44] [45]
3. How Did I Get Involved with System Dynamics Modeling?
Since my main area of research, the effect of state capacity and conflict on development, lies at the intersection of international relations, development, and economics, I have had intensive training in economics during my undergraduate and graduate studies. I have an undergraduate degree in economics,[46] which was followed by a PhD in Political Science and Economics. Many economics classes involve some degree of mathematics, which helped me become familiar with mathematical models and quantitative methods. As a result of my academic background, one may think that I was already in an advantageous position to learn advanced modeling skills. However, as I argue throughout this article, most types of modeling in international relations do not necessarily require previous knowledge of advanced mathematics. The main prerequisite for learning these models is having a systematic and analytical way of thinking. In this regard, the main benefit of my previous economics training when I started learning about modeling probably was having a higher than average self-confidence, which turned out to be groundless.
Although I had previously taken some classes that included formal models, including several economic growth models and game theory, the first time I was introduced to system dynamics modeling was when I took a summer class on differential equations in graduate school. I took this class on the recommendation of my PhD advisor. His reasoning was that in some branches of peace science in which I was interested, such as the deterrence theory or evolution of power and state capacity, being knowledgeable about modeling is particularly useful because data in these fields are either low-quality or non-existent. He insisted that taking this class would teach me the mathematical foundations needed to learn more advanced modeling and simulation techniques. Indeed, the differential equations class was followed by seminars in complexity, dynamic modeling, and agent-based modeling.
Currently, many political science or international relations graduate programs all over the world offer courses on complexity, modeling, and simulation. In addition to directly taking classes from international relations or political science departments, one can also find courses on modeling in different departments, including mathematics or computer science. Further study of these methods can also be carried on in short-term courses of the Inter-university Consortium for Political and Social Research (ICPSR) or the European Consortium of Political Research (ECPR) as well as via the programs and annual conferences of the Computational Social Science Society of the Americas, the European Social Simulation Association, or the System Dynamics Society. Participating in these courses or conferences not only helps one get acquainted with these methods, but it is also useful for meeting researchers with similar methodological interests from different fields of study, which can result in fruitful collaborations.
The assertion that formal models, dynamic models, and simulations have a steep learning curve and there is little payoff to learning these methodologies is a misconception. In fact, the nature of formal modeling is quite similar to the nature of qualitative research in the sense that theorizing in both traditions starts by simplifying descriptions, establishing concepts, and endeavoring to reach generalizations. So, these models should be considered as a way of thinking rather than a set of complex techniques. Just like the majority of the researchers working with statistics cannot (and do not need to) solve the sophisticated methods they use, one does not have to have a perfect command on all the intricacies of dynamic models, especially for using these models in applied analyses. After understanding the logic and working principles of dynamic models, one can learn using one of the free or paid ODE solvers mentioned in the following paragraphs, which are increasingly accessible due to the rapid increase in the number of instructive videos, websites, or applications.
Since the early days of my undergraduate education, I have always been mainly interested in quantitative methods. Still, I had not considered pursuing system dynamics models and complexity research until my advisor forced me to take the differential equations class I mentioned above. When the class started, at first, I thought the complexity and abstractness of some of the readings were overwhelming. However, after getting used to the structure, I realized that this is not different than learning a new language. The best thing about this language was that I did not need to learn all the vocabulary, because the computer programs I mentioned above were generating the sentences for me. Another really useful aspect of these methods is the close-knit structure of the academic community. The organizations that I mentioned in this section are relatively small in size, but they frequently hold research and training workshops. Moreover, almost all of the members are incredibly encouraging, and they have an extraordinary support group for all levels of learners.
Nevertheless, learning these models is likely to be challenging, at least in its earlier stages, particularly for people who have never dealt with mathematics or some sort of modeling before. Considering many students of international relations fall into this category, it is not surprising that system dynamics modeling, or modeling in general, has been a small subsection of international relations methodology up to now. No matter whether one chooses to take courses or learn these methods by herself, I have three sets of advice, based on my personal experience, which can potentially be helpful throughout the process.
First, developing theoretical skills to go in hand in hand with system dynamics modeling is crucial. On one hand, the primary task of social scientists is theory development. Thus, system dynamics modeling is only a tool to assist the researcher in providing answers to the questions related to her research program. So, international relations or social science theory should not take a backseat, especially in the earlier parts of the career. On the other hand, system dynamics modeling is only one type of modeling within the toolbox of available methods. The majority of the social science scholars who work with system dynamics modeling are also knowledgeable on several other models. In this regard, learning additional methods as well as modeling techniques and principals is likely to improve the quality of the overall research by providing alternatives for each research question. Thus, it is a good idea to consider taking courses including - but not limited to - game theory, complexity, the logic of algorithms (and genetic algorithms), formal modeling, agent-based modeling, and simulation techniques.[47]
Second, as discussed above, system dynamics is a computer-aided approach in social sciences. Consequently, being familiar with some major computer programs and investing in technical skills is the key to success for doing system dynamics modeling or modeling in general. Numerous programs focus on different types of models. Several programs are capable of solving system dynamics models. Some of these programs are free to use while others require a fee for purchasing. The most frequently used programs that have to be paid for include MathLab, WolframAlpha, Wolfram Mathematica, and Maple. On the other hand, there are free alternatives to these programs. Although the free programs generally are not able to create extravagant graphs like the paid alternatives, they do cover the basics of solving a set of lower or higher order ODEs using Euler’s, Runge-Kutta, Bursch-Stoller and other methods. These free alternatives include the ODE Toolkit, Octave-Forge, or dCode. Another alternative is to write your own program (or find one of the existing packages) using R, C++, Python, or Java.
Modeling and quantitative research can be considered as an ecosystem. Many models are either complements or constitute the foundations of other models. In more advanced modeling settings, different models can be nested within each other. For these reasons, one should also consider investing in data visualization and simulation skills, in addition to the programs mentioned above, some of which are also capable of data visualization of running simulations. For example, learning geographic information systems software, including GRASS GIS, QGIS, or ArcGIS, is useful for developing models and simulations with a geospatial content. Tableau and SigmaPlot are useful for visualizing and analyzing any type of data. Repast, Swarm, or Vensim are useful for running agent-based models. There are many different modeling techniques and software. So, as one digs deeper in a modeling perspective, she will find the most suitable specific software that meets her needs.
Third, like the rest of graduate school and academia, probably the most crucial skills to master (system dynamics) modeling are related to personal and psychological traits. Learning a new model can be difficult. There will be much blood, sweat, and tears before grasping the fundamentals of modeling, and even after then, it will sometimes be tough to come up with an original model that sufficiently captures the reality. For this reason, starting the learning process with a high level of motivation, persisting on trying even after several failures, and being patient is essential for becoming proficient. Also related to the personal traits, it is also essential to remember networking and forming a group of collaborators or friends that are available for help or consultation when the modeling is stuck.
4. Developing System Dynamics Models
In this section, I discuss several aspects that are important in developing system dynamics models in addition to demonstrating the process by a building dynamic model and giving examples of several more sophisticated models.
To show the setup, let’s consider a simple arms race model. First modeled by Lewis Richardson,[48] the basic arms race model assumes that the level of a country’s military expenditures is proportional to the military expenditures of its rival, but restrained by domestic or economic constraints the country faces. We can set up the system with the following two equations:

In these equations, x and y represent the military expenditures of two countries at time t. The constants a and b depict the intensity of the rivalry (or how much a country fear its rival), m and n depict the scale of the constraints (domestic economy, interest groups, etc.), and r and s depict the existing level of enmity or distrust against the other country that would carry on even if military expenditures were wholly cut (negative values for r and s would represent the feelings of neighborliness or friendliness).
Although this is an elementary model and a significant simplification of the reality, several results emerge from this model. It can be observed that the military expenditures of the two countries are interdependent. The evolution of the military spending in each country ultimately depends on how much its rival spends, how much the countries fear each other, and how much the countries distrust each other. In the equilibrium, countries may choose to disarm entirely on one extreme. On the other extreme, if they sufficiently fear and distrust each other, each country might keep increasing its spending to cause an endless spiral of increases. Alternatively, they might end up at a stable equilibrium somewhere in the middle. More detailed explanations and discussions of implications of the basic arms race model can be found in Zinnes and Gillespie[49] and Intriligator and Brito.[50]
The basic arms race model can be demonstrated using the following causal diagram, drawn using Vensim:
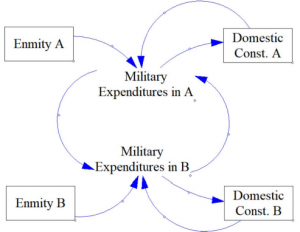
Figure 1: Causal Diagram of the Basic Arms Race Model
This causal diagram in Figure 1 represents equations (1) and (2) explained above. The arrows show the direction of the relationship. This model does not include the positive and negative signs because Vensim’s simulation mechanism does not require these signs near the arrows as they are defined within the variables.
The arms race model can easily be expanded in a system dynamic setting to make the model more realistic and the results and forecasts more accurate using additional variables and interactions. In Figure 2, such a model is presented. This more sophisticated model considers the economic capacity and total armament as stock variables, affected by flow variables like the economic growth, desired strength ratio, investment, and depreciation. These additional variables are connected to each other within the system of each country. In addition, the systems of two countries are connected to each other via the total armament and target armament variables.
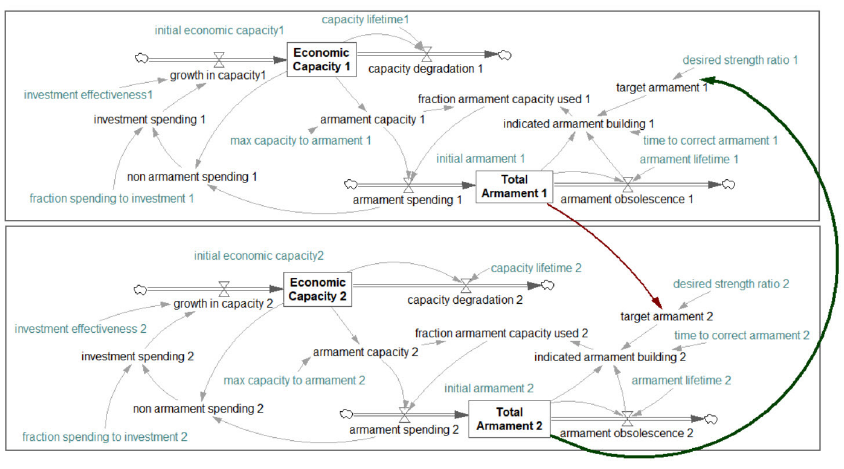
Figure 2: Causal Diagram of the Arms Race Model with Additional Variables
As discussed above, models are only a simplification of reality. One of the early projects of system dynamics, Industrial Dynamics, had 60 levels and almost 250 variables.[51] On the other hand, a similar model, Urban Dynamics, successfully explained the causes of urban boom or decay with 3 levels and 9 principal variables.[52] Whereas models like Industrial Dynamics or the arms race model in Figure 2 are more common in public or defense policy, operations management, manufacturing, and the industry, many theoretical scientific models tend to be relatively straightforward. This has to do with the properties of a good theory, particularly the importance of parsimony.[53] More complicated models do not necessarily bring along scientific superiority. Particularly in the system dynamics setting and modeling social dynamics, building overly complex models can cause some of the variables to “explode,” that is, showing infinite growth or quick decay behavior, which causes the rest of the model to misbehave. Moreover, smaller models are more accessible and easier to understand. Thus, gaining insights from smaller models is easier and often more rewarding.[54]
Lastly, I present a model that I developed on the spread of intrastate war. This model takes a spread of disease model from epidemiology and extends it to explain the mechanism through which an intrastate conflict is spread from an "infected" country to a "susceptible" country. It shows that refugees can act as the channels to carry the conflict disease from the initial country by disturbing economic and social dynamics of the host whereas the state capacity of the host country acts as the immunity system.
I set this system up as a set of five differential equations. In these equations, evolution of conflicts in both the initial country (country a) and a country b that shares a border with country a are endogenous. Economic conditions in both countries and the flow of refugees are also modeled as endogenous variables. On the other hand levels of democracy, state capacity (represented by Relative Political Capacity, or RPC), and inequality in both countries are taken as exogenous variables.

This formal system described above is a deterministic process. Nevertheless, some researchers may argue that social dynamics are inherently probabilistic, not deterministic. Consequently, using stochastic approaches or probabilistic mathematics might be considered more appropriate when analyzing social phenomena. It is true that social dynamics often include stochastic components. However, even stochastic models are structured around a “deterministic core,” as Brown states.[55] Thus, using deterministic models, mainly to establish the initial understanding of the dynamic phenomena, is sufficient. As the research progresses, probabilistic behavior can be introduced using stochastic differential equations or running Monte Carlo Simulations.
Figure 3 demonstrates the set of interdependent, non-linear, first order differential equations that constitute the model. As the figure shows, the interdependent relationship between all variables is a highly complex one.
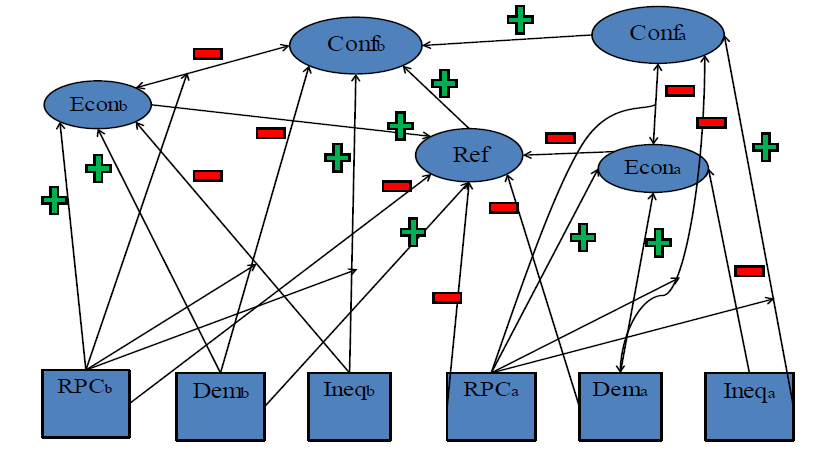
Figure 3: The depiction of the model
The set of differential equations are solved using a graphical ODE solver. Amongst the programs I discussed above, I use ODE Toolkit (v.1.4). I first run a baseline model for two theoretical less developed countries with average levels of state capacity (thus, with values of RPC = 0.3). The graph in Figure 4 represents the behavior of endogenous variables over time from their baseline. As we can see from the ODE output, the economy of Country a is shrinking as the level of conflict in Country a increases. As a result of the economic decline in Country a, the number of refugees coming from Country a to Country b increases. The increase of refugees in Country b leads to an increase in the level of conflict, which results in a decrease in economy.
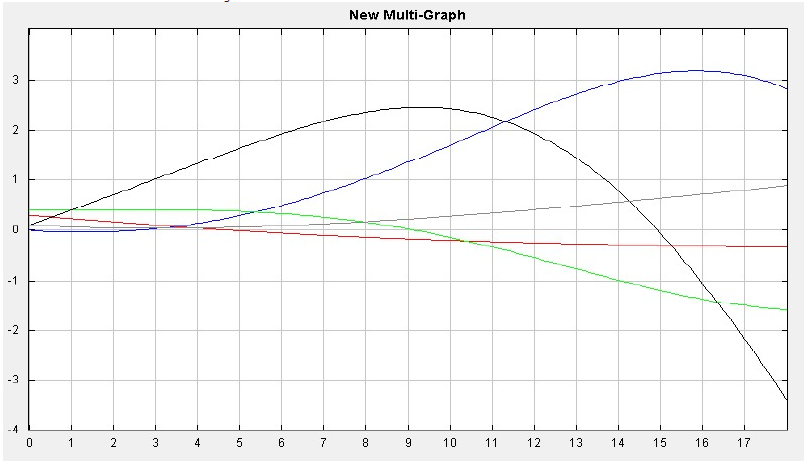
Figure 4: Trajectory for Mid_RPCa & Mid_RPCb, where the Blue line represents Conflict in B, Green line represents Economy of B, Black line represents Refugees, Red line represents Economy of A, and Grey line represents Conflict in A.
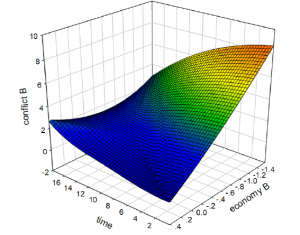
Figure 5: The 3D Visualization of Mid_RPCa & Mid_RPCb.
However, as the level of economy in Country b goes down, the country becomes less attractive to refugees, so the number of refugees decreases after the decline in the economy becomes apparent at time 10. The rate of decrease in refugees is high since the level of conflict increases rapidly, and the economy in Country b even becomes worse than the economy in Country a.
The 3D graph in Figure 5, drawn using SigmaPlot 12.5 with the results of the solutions of the ODEs, presents a visualization of the main variables. We can see that with a middle-level of RPC when the level of economy in b is low, the level of conflict in b remains at a high level. It first increases then decreases, because the number of refugees first increases then decreases due to the change of economy. However, when the level of economy in b is relatively high, the level of conflict slowly increases at a low level. Also, we can also see that as time passes and the level of economy decreases, the level of conflict increases.
One of the main advantages of system dynamics models is that after the model is set up, we can investigate different scenarios by changing the initial values of variables. Let’s demonstrate this by exploring what happens when we increase the level of state capacity of the neighboring country b from average to high. To do this, I increase the RPC in Country b to 0.45, while keeping other initial values same as before.
As we can see in Figure 6, the results change entirely. Although the levels of conflict and economy in Country a remain the same, those of Country b go to opposite directions. With the high level of RPC, the economy in Country b improves at a steady speed before period 13 and at an even higher speed after that. As the gap between Country a’s economy and Country b’s economy increases, the number of refugees going to Country b also becomes larger and larger. In the previous scenario, the level of conflict in Country b increases as the number of refugees increases. However, this time when RPC is high, the level of conflict in Country b does not increase. It even decreases after the economy improves sharply. It tells us that when the RPC is high, the country can handle a large (or larger) number of refugees without having higher levels of conflict.
The 3D graph in Figure 7 helps us understand this scenario better. Interestingly, when the level of the economy is low, the level of conflict first decreases rapidly then increases slightly, making a u-curve in the graph. However, when the level of the economy is high, the level of conflict is much higher, though it decreases at a steady speed. It is because the superb economy attracts too many refugees, which adds the likelihood of instability. What’s more, when looking at both the economy and conflict across time, the model shows that as the level of economy increases, the level of conflict does not change much. This is in line with the first postulate that high level of RPC in Country b will reduce the likelihood of intrastate conflict. Also, when the economy starts at a high level, the decrease in the economy over time also results in the decrease in the level of conflict.
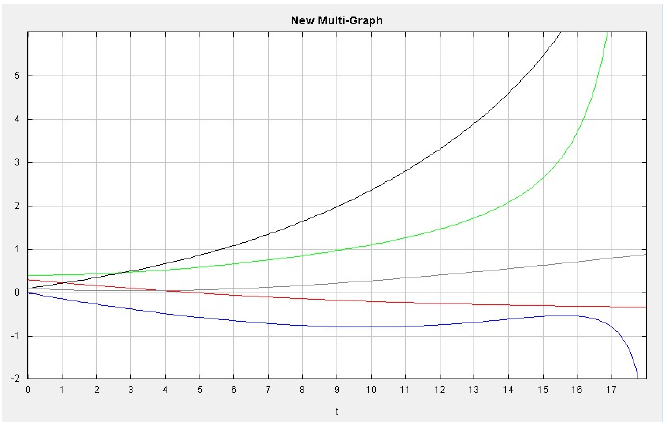
Figure 6: Trajectory for Mid_RPCa & High_RPCb, where the Blue line represents Conflict in B, Green line represents Economy of B, Black line represents Refugees, Red line represents Economy of A, and Grey line represents Conflict in A.
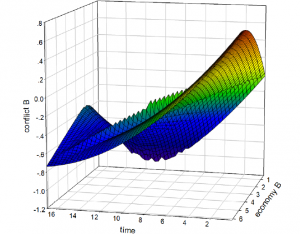
Figure 7: The 3D Visualization of Mid_RPCa & High_RPCb.
5. Conclusions
This article provides an introduction to system dynamics models with a particular focus on their applications on political science and international relations. As discussed throughout the article, a system dynamics approach has many advantages (and disadvantages). Methods in international relations, after all, are a means to an end. As international relations scholars, our priority should be to develop theories of world politics. Nevertheless, research methods are crucial instruments for us to approach different questions. Ultimately, I argue that system dynamics models are a useful and valuable addition to the methodological toolbox of students of international relations.
System dynamics models provide an interdisciplinary perspective bridging different fields in social sciences as well as social sciences and public policy, physical sciences, and engineering. The majority of the complex problems of the 21st century are not discipline-specific. Especially with increased physical and virtual interconnectedness, almost every decision creates multiple shock waves in many different areas. The butterfly effect is relevant today, more than ever. Thus, combining the knowledge and wisdom from different disciplines is crucial for dealing with modern problems.
The majority of the academic work in international relations and conflict studies in Turkey uses qualitative techniques, [56] [57] and formal models are an unambiguous minority with respect to the choice of methods.[58] However, quantitative techniques and modeling bring along many benefits, especially in recent years, in which the computational power has been growing geometrically. A few decades ago, only a few social scientists would be able to use system dynamics modeling, mainly due to the extremely high costs of entry; i.e., advanced mathematical skills. These barriers to entry have been significantly lowered in the recent years. Thus, we should observe, and have been observing, more extensive use of these methods.
Still, in my opinion, system dynamics approach should be treated as a complement rather than a substitute for “traditional” qualitative and quantitative methods. Personally, I still carry out the majority of my research using these traditional methods and inductive techniques. Each question requires a different design and knowing the advantages and disadvantages of all, or many, methods and designs help you choose the most appropriate one for the question and data you have.
Supplementing system dynamics modeling with simulations and learning alternative simulation techniques is the natural next step after mastering system dynamics modeling. Using microsimulations, queuing models, multilevel simulations, cellular automata, multi-agent (or agent-based) models, or learning models allow for including more levels to the simulation, controlling for communications between agents, modelling different and more complex types of agents.[59] Each of these features makes the model slightly more realistic, generating more accurate outcomes. These models can then be used for experimenting different policy choices and analyzing the effect of different choices on short- and long-term outcomes.
To my knowledge, this is the first paper that introduces the system dynamics approach in Turkish international relations and political science literature. As the methodological scope in Turkish academia widens, as well as the above-mentioned technical reasons for the increased use of nonlinear and system dynamics models, one can expect the more frequent use of such models. Understanding world politics from a multi-disciplinary and multi-method perspective is crucial for solving new types of emerging problems. Thus, the movement towards a more integrated approach is necessary. Fluency in not just one, but multiple quantitative, qualitative, and methodological approaches are essential to understanding the strengths and weaknesses of each. This will undoubtedly expand the topics that can be studied and enhance the relevance and pertinence of the works produced in Turkish academia in political and international academic domains.
[1] Oxford English Dictionary Online, s.v. “system,” accessed May 20, 2018, https://en.oxforddictionaries.com/definition/system.
[2] Nigel Gilbert and Klaus G. Troitzsch, Simulation for the Social Scientist (Second Edition) (Berkshire: Open University Press, 2005).
[3] Herbert A. Simon, Models of Man: Social and Rational (New York: Wiley, 1957).
[4] James S. Coleman, Introduction to Mathematical Sociology (New York: Free Press, 1964).
[5] Jay W. Forester, “Industrial Dynamics: A Major Breakthrough for Decision Makers,” Harvard Business Review 36, no. 4 (1958): 37–66.
[6] Despite population biology may at first sound irrelevant to social sciences, its main concern, the interaction of various life forms within an existing ecosystem, can be easily extended and implemented in social and political theories.
[7] Courtney Brown, Serpents in the Sand: Essays on the Nonlinear Nature of Politics and Human Destiny (Ann Arbor: The University of Michigan Press, 1995).
[8] Gary Goertz and James Mahoney, A Tale of Two Cultures: Qualitative and Quantitative Research in the Social Sciences (Princeton: Princeton University Press, 2012).
[9] Brown, Serpents in the Sand.
[10] Moreover, measures that range back over 50–100 years are mainly cruder ones such as Polity (which measures regime type or the level of democracy). More elaborate measures require more detailed components, which are not available for collection.
[11] Brown, Serpents in the Sand.
[12] Brown, Serpents in the Sand.
[13] George P. Richardson and David F. Andersen, “Systems Thinking, Mapping, and Modeling in Group Decision and Negotiation,” in Handbook of Group Decision and Negotiation, ed. D. Marc Kilgour and Colin Eden (Dordrecht: Springer, 2010).
[14] Susan Howick et al., “Linking Event Thinking with Structural Thinking: Methods to Improve Client Value in Projects,” System Dynamics Review 22, no. 2 (2006): 113–40.
[15] Yu-Che Chen and Michael J. Ahn, Routledge Handbook on Information Technology in Government (New York: Routledge, 2017).
[16] George P. Richardson, Feedback Thought in Social Science and Systems Theory (Philadelphia: University of Pennsylvania Press, 1991).
[17] Jay W. Forrester, “Market Growth as Influenced by Capital Investment,” Industrial Management Review 9, no. 2 (1968): 83–105.
[18] Ben S. Bernanke and Frederic S. Mishkin, “Inflation Targeting: A New Framework for Monetary Policy?,” Journal of Economic Perspectives 11, no. 2 (1997): 97–116.
[19] Craig W Kirkwood, System Dynamics Methods: A Quick Introduction (College of Business Arizona State University, 1998).
[20] Boris Urlanis, Wars and Population (Moscow: Progress Publishers, 1971).
[21] Ali Fisunoglu, “Beyond the Phoenix Factor: Consequences of Major Wars and Determinants of Postwar Recovery” (PhD diss., Claremont Graduate University, 2014).
[22] Henrik Urdal, “A Clash of Generations? Youth Bulges and Political Violence,” International Studies Quarterly 50, no. 3 (2006): 607–29.
[23] Thomas C. Schelling, “Social Mechanisms and Social Dynamics,” in Social Mechanisms: An Analytical Approach to Social Theory, ed. Peter Hedstrom and Richard Swedberg (Cambridge: Cambridge University Press, 1998), 32–44.
[24] A.F.K. Organski et al., Births, Deaths, and Taxes: The Demographic and Political Transitions (Chicago: The University of Chicago Press, 1984).
[25] A.F.K Organski, World Politics (New York: Alfred A. Knopf, 1968).
[26] Lewis F. Richardson, Arms and Insecurity: A Mathematical Study of the Causes and Origins of War (Pittsburgh: Boxwood, 1960).
[27] Robert Jervis, System Effects: Complexity in Political and Social Life (Princeton: Princeton University Press, 1997)
[28] Kelly M. Kadera, “Transmission, Barriers, and Constraints: A Dynamic Model of the Spread of War,” Journal of Conflict Resolution 42, no. 3 (1998): 367–87.
[29] Kelly M. Kadera and Daniel S. Morey, “The Trade–Offs of Fighting and Investing: A Model of the Evolution of War and Peace,” Conflict Management and Peace Science 25, no 2 (2008): 152–70.
[30] Dina A. Zinnes and Robert G. Muncaster, “The Dynamics of Hostile Activity and the Prediction of War,” Journal of Conflict Resolution 28, no. 2 (1984): 187–229.
[31] Mark A. Abdollahian, Michael Baranick, Brice Nicholson, and Matt Nickens, “A Formal Model of Stabilization and Reconstruction Operations,” Military Operations Research 14, no. 3 (2009): 5–30.
[32] David S. Morey, “When War Brings Peace: A Dynamic Model of the Rivalry Process,” American Journal of Political Science 55, no. 2 (2011): 263–275.
[33] National Consortium for the Study of Terrorism and Responses to Terrorism (START), Global Terrorism Database [Data file] (2017), https://www.start.umd.edu/gtd.
[34] Joao Ricardo Faria and Daniel G. Arce M., “Terror Support and Recruitment,” Defence and Peace Economics 16, no. 4 (2005): 263–73.
[35] Dean Hoover and David Kowalewski, “Dynamic Models of Dissent and Repression,” The Journal of Conflict Resolution 36, no. 1 (1992): 150–82.
[36] Todd Chamberlain, “Systems Dynamics Model of Al-Qa'ida and United States ‘Competition,’” Journal of Homeland Security and Emergency Management 4, no. 3 (2007): 1–23.
[37] Larry Blank et al., “A Dynamic Model of Insurgency: The Case of the War in Iraq,” Peace Economics, Peace Science and Public Policy 14, no. 2 (2008): 1–26.
[38] Catherine M. Banks and John A. Sokolowski, “From War on Drugs to War against Terrorism: Modeling the Evolution of Colombia’s Counter-Insurgency,” Social Science Research 38, no. 1 (2009): 146–54.
[39] Kelly M. Kadera and Sang-Ki Kim, “Breaking Natural Selection: A Dynamic Model of Civil War and Third-Party Intervention,” (paper presented at the EPSA 2013 Annual Conference, Paper 862, Barcelona).
[40] Viktoria Spaiser et al., “The Dynamics of Democracy, Development and Cultural Values,” PloS ONE 9, no. 6 (2014): e86468.
[41] Mark A. Abdollahian et al, “Dynamics of Cultural Change: The Human Development Perspective,” International Studies Quarterly 56, no. 4 (2012): 827–42.
[42] Adam Przeworski and John Sprague, Paper Stones: A History of Electoral Socialism (Chicago: University of Chicago Press, 1986).
[43] Courtney Brown, Ballots of Tumult: A Portrait of Volatility in American Voting (Ann Arbor: The University of Michigan Press, 1991).
[44] Peder Hjorth and Ali Bagheri, “Navigating Towards Sustainable Development: A System Dynamics Approach,” Futures 38, no. 1 (2006): 74–92.
[45] Thierry Malleret, Disequilibrium: A World Out of Kilter (Amazon Kindle Edition, 2012).
[46] I was originally double majoring with International Relations, but I decided to drop the double major after being admitted to a PhD program in my senior year, mainly to avoid the required Constitutional Law class.
[47] These courses mostly focus on the deductive aspects of research design. In addition to these, taking several courses on probability and statistics would enable the researcher to incorporate stochasticity in the models and/or test the propositions derived from these models with actual data.
[48] Richardson, Arms and Insecurity.
[49] John V. Gillespie and Dina A. Zinnes, eds., Mathematical Systems in International Relations Research (New York: Praeger Publishers, 1977).
[50] Michael D. Intriligator and Dagobert L. Brito, “Arms Races,” Defence and Peace Economics 11, no. 1 (2000): 45–54.
[51] Jay W. Forrester, Industrial Dynamics (Cambridge: The M.I.T. Press, 1961).
[52] Jay W. Forrester, Urban Dynamics (Cambridge: The M.I.T. Press, 1969).
[53] W. Phillips Shively, The Craft of Political Research (10th Edition) (New York: Routledge, 2017).
[54] Navid Ghaffarzadegan et al., “How Small System Dynamics Models Can Help the Public Policy Process,” System Dynamics Review 27, no. 1 (2011): 22–44
[55] Courtney Brown, Differential Equations: A Modeling Approach (Thousand Oaks: Sage, 2007).
[56] Oner Akgul, “A Bibliographical Study on the Academic Research of Peace and Conflict in Turkey,” (paper presented at the 7th Eurasian Peace Science Meeting, İstanbul, 2018).
[57] Cenker Korhan Demir and Engin Avcı, “Turkish Terrorism Studies: A Preliminary Assessment,” All Azimuth 7, no. 1 (2018): 21–44.
[58] Mustafa Aydin, Fulya Hisaroglu, and Korhan Yazgan, “Türkiye'de Uluslararası İlişkiler Akademisyenleri ve Alana Yönelik Yaklaşımları Üzerine Bir İnceleme: TRIP 2014 Sonuçları,” Uluslararasi Iliskiler 12, no. 48 (2016): 3–35.
[59] Gilbert and Troitzsch, Simulation for the Social Scientist.
Abdollahian, Mark A., et al. “A Formal Model of Stabilization and Reconstruction Operations.” Military Operations Research 14, no. 3 (2009): 5–30.
———. “Dynamics of Cultural Change: The Human Development Perspective.” International Studies Quarterly 56, no. 4 (2012): 827–42.
Akgul, Oner. “A Bibliographical Study on the Academic Research of Peace and Conflict in Turkey.” Paper presented at the 7th Eurasian Peace Science Meeting, İstanbul, 2018.
Aydin, Mustafa, Fulya Hisaroglu and Korhan Yazgan. “Türkiye'de Uluslararası İlişkiler Akademisyenleri ve Alana Yönelik Yaklaşımları Üzerine Bir İnceleme: TRIP 2014 Sonuçları.” Uluslararasi Iliskiler 12, no. 48 (2016): 3–35.
Banks, Catherine M., and John A. Sokolowski. “From War on Drugs to War against Terrorism: Modeling the Evolution of Colombia’s Counter-Insurgency.” Social Science Research 38, no. 1 (2009): 146–54.
Bernanke, Ben S., and Frederic S. Mishkin. “Inflation Targeting: A New Framework for Monetary Policy?” Journal of Economic Perspectives 11, no. 2 (1997): 97–116.
Blank, Larry, et al. “A Dynamic Model of Insurgency: The Case of the War in Iraq.” Peace Economics, Peace Science and Public Policy 14, no. 2 (2008): 1–26.
Brown, Courtney. Ballots of Tumult: A Portrait of Volatility in American Voting. Ann Arbor: The University of Michigan Press, 1991.
———. Differential Equations: A Modeling Approach. Thousand Oaks: Sage, 2007.
———. Serpents in the Sand: Essays on the Nonlinear Nature of Politics and Human Destiny. Ann Arbor: The University of Michigan Press, 1995.
Chamberlain, Todd. “Systems Dynamics Model of Al-Qa'ida and United States ‘Competition’.” Journal of Homeland Security and Emergency Management 4, no. 3 (2007): 1–23.
Chen, Yu-Che, and Michael J. Ahn. Routledge Handbook on Information Technology in Government. New York: Routledge, 2017.
Coleman, James S. Introduction to Mathematical Sociology. New York: Free Press, 1964.
Demir, Cenker Korhan, and Engin Avci. “Turkish Terrorism Studies: A Preliminary Assessment.” All Azimuth 7, no. 1 (2018): 21–44.
Faria, Joao Ricardo, and Daniel G.M. Arce. “Terror Support and Recruitment.” Defence and Peace Economics 16, no. 4 (2005): 263–73.
Fisunoglu, Ali. “Beyond the Phoenix Factor: Consequences of Major Wars and Determinants of Postwar Recovery.” PhD Diss., Claremont Graduate University, 2014.
Forrester, Jay W. Industrial Dynamics. Cambridge: The M.I.T. Press, 1961.
———. “Industrial Dynamics: A Major Breakthrough for Decision Makers.” Harvard Business Review 36, no. 4 (1958): 37–66.
———. “Market Growth as Influenced by Capital Investment.” Industrial Management Review 9, no. 2 (1968): 83–105.
———. Urban Dynamics. Cambridge: The M.I.T. Press, 1969.
Ghaffarzadegan, Navid, John Lyneis, and George P. Richardson. “How Small System Dynamics Models Can Help the Public Policy Process.” System Dynamics Review 27, no. 1 (2011): 22–44.
Gilbert, Niger, and Klaus G. Troitzsch. Simulation for the Social Scientist (Second Edition). Berkshire, England: Open University Press, 2005.
Gillespie, John V., and Dina A. Zinnes. Mathematical Systems in International Relations Research. New York: Praeger Publishers, 1977.
Goertz, Gary, and James Mahoney. A Tale of Two Cultures: Qualitative and Quantitative Research in the Social Sciences. Princeton: Princeton University Press, 2012.
Hjorth, Peder, and Ali Bagheri. “Navigating Towards Sustainable Development: A System Dynamics Approach.” Futures 38, no. 1 (2006): 74–92.
Hoover, Dean and David Kowalewski. "Dynamic Models of Dissent and Repression." The Journal of Conflict Resolution 36.1 (1992): 150–182.
Howick, Susan, Fran Ackermann, and David Andersen. “Linking Event Thinking with Structural Thinking: Methods to Improve Client Value in Projects.” System Dynamics Review 22, no. 2 (2006): 113–40.
Intriligator, Michael D., and Dagobert L. Brito. “Arms Races.” Defence and Peace Economics 11, no. 1 (2000): 45–54.
Jervis, Robert. System Effects: Complexity in Political and Social Life. Princeton: Princeton University Press, 1997.
Kadera, Kelly M. “Transmission, Barriers, and Constraints: A Dynamic Model of the Spread of War.” Journal of Conflict Resolution 42, no. 3 (1998): 367–87.
Kadera, Kelly M., and Daniel S. Morey. “The Trade-Offs of Fighting and Investing: A Model of the Evolution of War and Peace.” Conflict Management and Peace Science 25, no. 2 (2008): 152–70.
Kadera, Kelly M., and Sank-Ki Kim. “Breaking Natural Selection: A Dynamic Model of Civil War and Third-Party Intervention.” EPSA 2013 Annual Conference Paper 862 (2013).
Kirkwood, Craig W. System Dynamics Methods: A Quick Introduction. College of Business, Arizona State University, 1998.
Malleret, Thierry. Disequilibrium: A World Out of Kilter. Amazon Kindle Edition, 2012.
Morey, David S. “When War Brings Peace: A Dynamic Model of the Rivalry Process.” American Journal of Political Science 55, no. 2 (2011): 263-75.
Organski, A.F.K. World Politics. New York: Alfred A. Knopf, 1968.
Organski, A.F.K., et al. Births, Deaths, and Taxes: The Demographic and Political Transitions. Chicago: The University of Chicago Press, 1984.
Przeworski, Adam, and John Sprague. Paper Stones: A History of Electoral Socialism. Chicago: The University of Chicago Press, 1986.
Richardson, George P. Feedback Thought in Social Science and Systems Theory. Philadelphia: University of Pennsylvania Press, 1991.
Richardson, George P., and David F. Andersen. “Systems Thinking, Mapping, and Modeling in Group Decision and Negotiation.” Handbook of Group Decision and Negotiation, edited by Marc D. Kilgour and Colin Eden, 313–24. Dordrecht: Springer, 2010.
Richardson, Lewis F. Arms and Insecurity: A Mathematical Study of the Causes and Origins of War. Pittsburgh: Boxwood, 1960.
Schelling, Thomas C. “Social Mechanisms and Social Dynamics.” In Social Mechanisms: An Analytical Approach to Social Theory, edited by Peter Hedstrom anf Richard Swedberg, 32–44. Cambridge: Cambridge University Press, 1998.
Shively, W. Phillips. The Craft of Political Research (10th Edition). New York: Routledge, 2017.
Simon, Herbert A. Models of Man: Social and Rational. New York: Wiley, 1957.
Spaiser, Viktoria, et al. “The Dynamics of Democracy, Development and Cultural Values.” PLoS ONE 9, no. 6 (2014): e97856.
Urdal, Henrik. “A Clash of Generations? Youth Bulges and Political Violence.” International Studies Quarterly 50, no. 3 (2006): 607–29.
Urlanis, Boris. Wars and Population. Moscow: Progress Publishers, 1971.
Zinnes, Dina A., and Robert G. Muncaster. “The Dynamics of Hostile Activity and the Prediction of War.” The Journal of Conflict Resolution 28, no. 2 (1984): 187–229.

